|
Итак, найдем минимальное значение функции цели при i=9, используя основное функциональное уравнение Беллмана (3.1):


Рисунок 3.2 - Сетевая модель шага 1
Шаг 2
В вектор состояния входят 3 узла:

Узел (4,6) соответствует г. Ульяновску, (5,5) - г. Саранск, (6,4) - г. Нижний Ломов.
Из узлов (4,6) и (6,4) путь в смежные с ними узлы однозначен. Обходной путь существует, но он не оптимален.
Стоимость прокладки дороги из г. Ульяновска и г. Ниж. Ломов в конечный пункт
г. Самару равна:

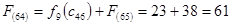
Из узла (5,5) г. Саранска можно продолжить дорогу к пункту В либо через (5,6)
г. Сызрань, либо через (6,5) г. Кузнецк.
Путь из г. Саранска в г. Самару через г. Сызрань складывается из суммы работ:

Путь из г. Саранска в г. Самару через г. Кузнецк складывается из суммы работ:
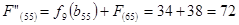
Сравниваем два значения и выбираем наименьшее значение. В данном случае выбираем маршрут, проходящий через г. Сызрань
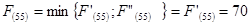
При выборе оптимального маршрута достаточно знаний прокладывания маршрута в пункт В из (4,6), (5,5), (6,4).
Найдем минимальное значение функции цели (оптимальный маршрут) при i=8, используя основное функциональное уравнение Беллмана (3.1):

Рисунок 3.3 - Сетевая модель шага 2
Шаг 3
В вектор состояния входят 4 узла:

Узел (3,6) - г. Уфа, (4,5) - г. Пенза, (5,4) - г. Тамбов, (6,3) - Воронеж
Из узлов (3,6) и (6,3) путь в смежные с ними узлы однозначен. Обходной путь существует, но он не оптимален.
Стоимость прокладки дороги из г. Уфы и г. Воронежа в конечный пункт г. Самару равна:
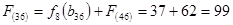
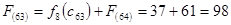
А для г. Пензы и г. Тамбова следует рассмотреть по 2 варианта маршрута.
Из узла (4,5) г. Пензы можно продолжить дорогу к пункту В либо через (4,6)
г. Ульяновск, либо через (5,5) г. Саранск.
Путь из г. Пензы в г. Самару через г. Ульяновск складывается из суммы работ:
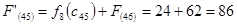
Путь из г. Пензы в г. Самару через г. Саранск складывается из суммы работ:
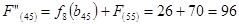
Сравниваем два значения и выбираем наименьшее значение. В данном случае выбираем маршрут, проходящий через г. Ульяновск

Из узла (5,4) г. Тамбова можно продолжить дорогу к пункту В либо через (6,4)
Путь из г. Тамбова в г. Самару через г. Саранск складывается из суммы работ:
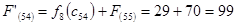
Путь из г. Тамбова в г. Самару через г. Ниж. Ломов складывается из суммы работ:
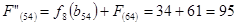
Сравниваем два значения и выбираем наименьшее значение. В данном случае выбираем маршрут, проходящий через г. Ниж. Ломов

При выборе оптимального маршрута достаточно знаний прокладывания маршрута в пункт В из (3,6), (4,5), (5,4), (6,3).
Найдем минимальное значение функции цели (оптимальный маршрут) при i=7, используя основное функциональное уравнение Беллмана (3.1):
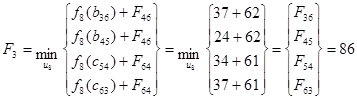
Перейти на страницу: 1 2 3 4 5 6 7 8 |