|
Для оценки качества полученных прогнозов используется следующий прием. Весь исходный для расчетов период времени делится на две части. Одна из них, охватывающая более ранний период времени и включающая не менее 2/3 уровней динамического ряда, используется для расчета параметров модели. Другая, более поздняя, часть временного периода используется для контроля за прогнозом, т.е. принимается условно за прогнозируемый период. Рассчитанные "прогнозные" значения соответствующего показателя на каждый год условно прогнозируемого периода сопоставляются с фактическими. Разности между ними представляют ошибки прогноза.
Для определения размеров погрешностей или точности прогноза показателя Y за весь условный прогнозируемый период может использоваться коэффициент несоответствия Тейла:
КТ=  (1.33) (1.33)
где Yi - фактическое значение показателя;
 - прогнозное значение показателя; - прогнозное значение показателя;
Пр - продолжительность условного прогнозируемого периода (число лет).
Числителем этого коэффициента является средняя квадратическая ошибка прогноза, а знаменателем - квадратный корень из среднего квадрата фактических значений показателя за условный прогнозируемый период. Этот показатель изменяется от 0 до 1. Чем ближе его значение к 0, тем лучше результаты прогнозирования.
Проверку статистической значимости модели можно осуществлять с помощью дисперсионного анализа, который позволяет установить, изменяется ли соответствующий показатель в значительной мере под влиянием отобранных факторов или это изменение носит случайный характер.
С этой целью дисперсия по факторам  сравнивается с остаточной дисперсией сравнивается с остаточной дисперсией  : :
 = =  , ,  = = (1.34) (1.34)
где Yi - фактическое значение моделируемого показателя - средняя арифметическая фактических значений показателя (за моделируемый период времени);
 - расчетное значение показателя, т.е. полученное из уравнения регрессии;- число наблюдений;- количество параметров в уравнении регрессии. - расчетное значение показателя, т.е. полученное из уравнения регрессии;- число наблюдений;- количество параметров в уравнении регрессии.
Определяется расчетное значение критерия Фишера
=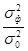 (1.35) (1.35)
которое затем сравнивается с F табличным, найденным для заданного уровня значимости q (обычно берут равным 0,05 или 0,01) для степеней свободы числителя (m-2) и знаменателя (n - m-1). Если расчетное F больше F табличного, то полученное уравнение регрессии статистически значимо.2.
Расчетная часть
Оценить степень влияния фактора X, влияющего на выходной показатель Y.
Таблица 2.1 - Динамика отдельных показателей развития. |
Год |
Y |

|

|

| |
1 |
2 |
3 |
4 |
5 | |
1 |
3,14 |
51,5 |
108,4 |
78,5 | |
2 |
3,18 |
55 |
107 |
78 | |
3 |
3,37 |
59,6 |
108,4 |
78,7 | |
4 |
3,26 |
61,6 |
107,9 |
78,4 | |
5 |
3,18 |
66,6 |
103,3 |
78,1 | |
6 |
3,2 |
76,5 |
111,5 |
77,2 | |
7 |
3,13 |
81,3 |
107,3 |
76,5 | |
8 |
3,02 |
84 |
107 |
76,1 | |
9 |
3,05 |
92,8 |
104,7 |
75,9 | |
10 |
3 |
97,2 |
107,1 |
75,2 | |
11 |
2,9 |
105,6 |
108,6 |
74,6 | |
12 |
2,86 |
107,1 |
104,5 |
75,5 | |
13 |
2,8 |
110,5 |
103,7 |
75,3 | |
14 |
2,74 |
120,1 |
106 |
74,8 | |
15 |
2,7 |
120,1 |
100,7 |
74,6 | |
16 |
2,63 |
130,2 |
102,2 |
73,8 | |
17 |
2,55 |
149,4 |
103,7 |
74,5 | |
18 |
2,5 |
157,2 |
103,5 |
74,6 | |
19 |
2,44 |
166,5 |
105,6 |
74,2 | |
20 |
2,38 |
170,1 |
102 |
74 |
Перейти на страницу: 1 2 3 4 5 6 |