|
Теория графов - раздел дискретной математики, в котором анализируются различные потоки (товарные, денежные, информационные, материальные) путем представления их в виде сетей (совокупности вершим и дуг).
Обладая свойствами наглядности, теория графов представляет исследователю простой, доступный и эффективный инструмент построения моделей экономики (календарное и сетевое планирования, управление производственными и финансовыми потоками, оптимизация маршрутов различных процессов).
Задание:
На графе вершины I (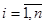 ) представляют состояние процесса производства запчастей для автомобилей марки BMW компанией ОАО «АвиаМоторс». Вершина 1 - I - вход соответствует началу производственного процесса. Вершина 8 - S - конец производственного процесса, в результате которого получаем готовые запчасти. Остальные вершины - события, совершаемые в процессе производства (плавление металла, обработка заготовки и т.д.). Дуги - работа, совершаемая для получения определенных событий. Весовые коэффициенты дуг - продолжительность (время) работы производственного процесса (амортизация оборудования, стоимость ручного и машинного труда, стоимость ресурсов, технологий, инноваций и информации - всё это используется в процессе производства).
Рисунок 4.1 - Граф задания
Таблица 4.1 - Весовые коэффициенты дуг |
n |
1,2 |
1,3 |
1,4 |
2,3 |
2,5 |
2,6 |
2,7 |
3,4 |
3,5 |
3,6 |
3,7 |
4,5 |
4,6 |
4,7 |
5,6 |
5,8 |
6,7 |
6,8 |
7,8 | |
12 |
0 |
6 |
5 |
7 |
N |
3 |
0 |
3 |
5 |
2 |
0 |
7 |
4 |
9 |
2 |
0 |
1 |
4 |
5 |
где n = 12 и N = 3.
Требуется:
. Провести анализ структуры графа. Установить, будет ли неориентированный граф, соответствующий заданному графу, эйлеровым. Разбить граф произвольным образом на два несвязных графа. Путем удаления наименее загруженных дуг:
● избавиться от циклов (если они есть в графе);
● построить дерево графа.
. Составить матрицы смежности (для неориентированного графа) и инциденций (для орграфа).
. Упорядочить нумерацию вершин графа, использую алгоритм Фалкерсона.
Перейти на страницу: 1 2 3 4 5 6 |
