|
В соответствии с пунктом 1 алгоритма на сети необходимо сформировать начальный поток. Опираясь на таблицу 4.2, составим маршрут, по которому проходит поток 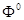 . Для составления маршрута будем двигаться от истока I=1 в направлении вершины с меньшими номерами до тех пор, пока не достигнем стока S=8 . Для составления маршрута будем двигаться от истока I=1 в направлении вершины с меньшими номерами до тех пор, пока не достигнем стока S=8
линейный транспортный задача граф
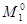 : 1 - (6)3- (3)4 - (7)5 - (2)6 - (1)7 - (5)8 : 1 - (6)3- (3)4 - (7)5 - (2)6 - (1)7 - (5)8
Максимальный поток, который может пройти по маршруту 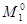 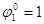 , величину общего потока ограничивает поток ребра (6,7), которое становится насыщенным. , величину общего потока ограничивает поток ребра (6,7), которое становится насыщенным.
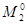 : 1 - (5)4 - (4)6 - (4)8 : 1 - (5)4 - (4)6 - (4)8
Максимальный поток, который может пройти по маршруту 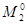  , величину общего потока ограничивают потоки ребер (4,6) и (6,8), которые становятся насыщенными , величину общего потока ограничивают потоки ребер (4,6) и (6,8), которые становятся насыщенными
.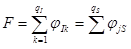 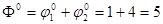
Составляем матрицу  , которая определяет пропускную способность сети при условии, что через нее проходит поток , которая определяет пропускную способность сети при условии, что через нее проходит поток  . Используя данные таблицы 4.3, составим маршруты дополнительных потоков, проходящие через ненасыщенные ребра. . Используя данные таблицы 4.3, составим маршруты дополнительных потоков, проходящие через ненасыщенные ребра.
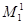 : 1 - (5)3 - (2)4 - (9)7 - (4)8 : 1 - (5)3 - (2)4 - (9)7 - (4)8
Максимальный поток, который может пройти по маршруту 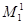 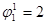 , величину общего потока ограничивает поток ребра (3,4), которое становится насыщенным. , величину общего потока ограничивает поток ребра (3,4), которое становится насыщенным.

Составляем матрицу 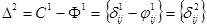 , которая определяет пропускную способность сети. , которая определяет пропускную способность сети.
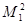 : 1 - (1)4 - (7)7 - (2)8 : 1 - (1)4 - (7)7 - (2)8
Максимальный поток, который может пройти по маршруту 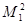  , величину общего потока ограничивает поток ребра (1,4), которое становится насыщенным. , величину общего потока ограничивает поток ребра (1,4), которое становится насыщенным.
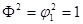
Составляем матрицу  , которая определяет пропускную способность сети. Для этого из элементов левой таблицы 4.4 вычитаем элементы правой. , которая определяет пропускную способность сети. Для этого из элементов левой таблицы 4.4 вычитаем элементы правой.
Так как больше маршрутов нет, заканчиваем решение и считаем максимальный поток.
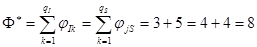

Рис. 4.7 - максимальные потоки и резервы дуг
. Сетевой граф
Сетевой граф - граф, вершины которого отображают состояния некоторого процесса (производство запчастей для автомобиля), а дуги - работы, ведущиеся в этом процессе. Каждой дуге сопоставляется время, за которое осуществляется работа и/или число рабочих, которые осуществляют работу.
В сетевом графе между начальным и конечным событиями может быть несколько путей.
Критический путь - непрерывная последовательность работ и событий от начального до конечного события, требующая наибольшего времени (затрат) для ее выполнения. Термин сетевого планирования, означающий самый длинный по временной протяженности путь в сетевом графе, определяющий продолжительность работ по выполнению проекта.
Перейти на страницу: 1 2 3 4 5 6 7 8 |