Проверка исходного ряда на стационарность

.

Оба условия выполняются. Согласно тесту Вальда-Вольфовитца гипотеза о постоянстве математического ожидания ряда не может быть отклонена.

Тест Манна - Уитни на постоянство математического ожидания

T1 = 150 - количество элементов в первой части ряда;

T2 = 212 - количество элементов во второй части ряда;

R1 = 26982 - сумма рангов, присвоенных элементам из первой части ряда

,

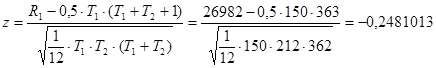В соответствии с тестом Манна-Уитни гипотеза о постоянстве математического ожидания не может быть отклонена.

Тест Сиджела-Тьюки на постоянство дисперсии

T1 = 150 - количество элементов в первой части ряда;

T2 = 212 - количество элементов во второй части ряда;

R1 = 26479 - сумма рангов, присвоенных элементам из первой части ряда

,

Согласно тесту Сиджела-Тьюки гипотеза о постоянстве дисперсии не может быть отклонена.

Итак, полученный ряд можно рассматривать как стационарный.

Эконометрические модели для конечных разностей

Идентификация модели

Изучив вид автокорреляционной и частной автокорреляционной функций ряда (таблица 5), полученного с помощью конечных разностей, можно предположить, какая модель наилучшим образом будет описывать процесс.

Таблица 5. Коррелограмма ряда третьих конечных разностей

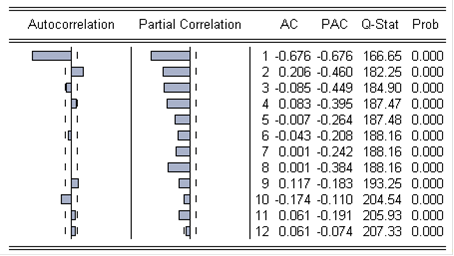
Первые два коэффициента автокорреляции ряда выходят за пределы доверительной трубки. Коэффициенты частной корреляции, вплоть до одиннадцатого включительно также выходят за пределы доверительной трубки, а их значения уменьшаются вплоть до шестого включительно.

Таблица 6. Критические значения для Q-Stat при уровне значимости 0,05

Критические значения, представленные в таблице 6, представляют собой квантиль хи квадрат распределения уровня значимости 0,05 со степенями свободы, равными количеству включаемых лагов («t» в таблице). Все значения Q-Stat (таблица 5) для ряда, полученного из исходного с помощью конечных разностей, превышают соответствующие критические значения (таблица 6). Это свидетельствует о наличии автокорреляции в полученном ряду, что позволит построить по нему модель, где в роли регрессоров выступают предыдущие значения ряда либо предыдущие значения ошибок модели.

Подобный вид автокорреляционной и частной автокорреляционной функций (таблица 5) характерен для моделей скользящего среднего второго порядка.

Поскольку ряд конечных разностей имеет распределение, отличное от нормального, критерий Стьюдента для определения статистической значимости коэффициентов в моделях использован быть не может.